复合材料由于其微观结构的非均匀性以及复杂的力学特性，使得其零部件设计难度大幅度提升。采用多尺度分析的方法，根据T300/Epoxy 斜纹机织复合材料细观几何参数，建立其单胞几何模型，引入周期性边界条件对单胞结构可以进行有限元分析，进而预测复合材料层合板三维弹性性能参数，并通过力学试验证明试验结果和预测结果较为接近；利用LS-Dyna 中的MAT_54建立复合材料渐进失效模型，通过三点弯曲试验结果调整模型参数，最终得到的复合材料渐进失效模型仿真结果与试验结果一致；将调整好的复合材料渐进失效模型应用到电动车复合材料车身骨架轻量化设计中，对复合材料骨架进行顶压仿真以及柱碰仿真分析。分析根据结果得出，复合材料车身骨架设计符合法规要求，与铝合金骨架相比，在重量减轻59%的同时表现出更好的耐撞性能。

  随着能源问题对人类带来的影响日益加剧，电动车的发展受到了更广泛的关注。但由于其电池重量过重，使得电动车的有效载荷过低，续航里程较小。未解决这一难题，能够最终靠轻量化技术，包括新材料的应用及结构优化等，减轻电动车的重量，达到降低能耗，提高续航能力的目的。由此可见轻量化技术对电动车的发展意义重大。纤维增强复合材料由于其较高的比强度、比刚度，在中倍受青睐。因此，对于复合材料汽车零部件及总成的设计与制造方法成为研究的热点。国内外学者通过理论、试验以及数值模拟的方法对复合材料的力学性能进行了系统的研究。MAMALIS 等针对复合材料薄壁管的耐撞性进行了系统的试验研究。试验根据结果得出应变率、纤维铺层顺序、纤维体积分数以及管的壁厚对结构的耐撞性能起决定性作用。YANG 等对3D 编织复合材料方管的吸能特性进行了深入的研究。NG 等用有限元法获得了机织复合材料二维本构模型，通过与试验对比验证该模型的正确性。左中鹅等针对平纹织物层合板细观结构建立了代表性体积元(Representative elemental volume, RVE)有限元模型，预测该复合材料模量，并根据失效准则对RVE 的强度进行预测。根据结果得出采用有限元预测的模量与实际值一致，单胞强度与实际强度吻合。DENG 等采用有限元数值仿真的方法对平纹玻璃纤维复合材料的弹性性能做多元化的分析，所得预测结果与试验结果相吻合。OBRADOVIC 等利用商用有限元软件LS-DYNA 对机织碳纤维增强复合材料进行建模，并将其运用到高速赛车的前端部件设计中。FEREBOLI 等利用LS-Dyna 中的MAT54 对复合材料波纹板有限元模型的建立进行了详细的介绍，并对其轴向压溃进行数值仿真，最后与试验作对比。MAMALIS 等对机织复合材料方管建立渐进失效有限元模型，并对其进行轴向静态和动态分析。

  由于复合材料出色的力学性能以及轻量化的优势，许多汽车制造公司开始研发制造复合材料汽车零部件及总成。兰博基尼公司推出整体式复合材料车身，使得该车型与上一代全铝车身相比减轻34kg。电动大巴制造公司在先进的车身制造工艺基础上，采用优化的方法获得了最佳复合材料车身结构，并使其重量达到最轻。然而上述关于汽车复合材料零部件及总成的报道均为结论性综述，关于具体的汽车复合材料零部件及总成的设计及性能分析方法却鲜有报道。

  本文旨在研究电动车复合材料车身的耐撞性能，通过与传统金属车身对比，进一步说明复合材料车身的优势。本文基于多尺度分析方法，针对斜纹机织碳纤维增强复合材料的细观几何结构，建立RVE 模型，采用有限元分析方法，引入周期性边界条件对层合板的弹性性能进行预测，通过力学试验对预测结果做验证(微观尺度)。利用商用有限元软件LS-DYNA 中的MAT_54 建立复合材料渐进失效模型，模拟复合材料试样三点弯曲工况，并通过试验结果调整仿真模型参数(介观尺度)。最后，将经过验证的复合材料渐进失效模型运用到电动车车身骨架轻量化设计中，比通过数值仿真分析与铝合金车身骨架进行性能对比(宏观尺度)。

  所有的机织物包含横纵交错的经纱和纬纱，依照结构的不同又可大致分为平纹机织、斜纹机织以及缎纹。本文研究的为T300碳纤维/环氧树脂斜纹机织复合材料，如图1 所示；为了更好地描述其几何结构，取单胞ABCD，其结构参数如图2 所示，截面参数如图3 所示。其中，A-B 面为x=0 的平面，A-D 面为y=0 的平面。单胞模型ABCD 厚度方向的中面为z=0 的平面。图2 中，hf、hw分别为纬纱和经纱在C-D面上的厚度值；hg为纬纱和经纱在厚度方向的距离；gw为经纱间的距离；gf为纬纱的距离。aw和af分别为经纱和纬纱的宽度。图3 中给出了A-D 截面的参数，其中弯曲位置(a1? a5)由以下方程确定。

  通过显微镜对图2 中的几何参数做测量，并对获得的几何结构可以进行计算得到纤维束中纤维体积分数Vfs，其结果如表1 所示。

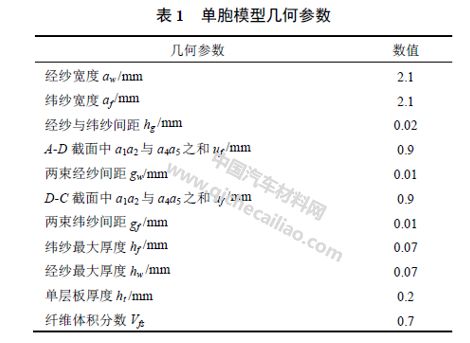
  纤维束是由纤维丝和树脂混合而成，可以将其等效为横观各向同性材料，因此能根据混合定律得出纤维束的等效弹性参数，如式(4)所示。

  式中，E1和E2分别为碳纤维束轴向及横向弹性模量；Ef1、Ef2为碳纤维丝轴向和横向的弹性模量，Vfs为纤维束中碳纤维的体积分数，Em为环氧树脂的弹性模量。Gf12和Gf23分别为碳纤维丝轴向及横向切变模量；G12、G23为碳纤维束轴向和横向的切变模量， Gm为环氧树脂切变模量。μf12为碳纤维束主泊松比，μm为环氧树脂泊松比。本文中斜纹机织复合材料所使用的T300碳纤维和环氧树脂的弹性性能参数如表2 所示。

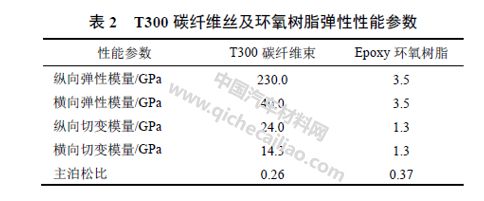
  通过对单包模型几何参数的测量，可以较为准确地建立斜纹机织复合材料的RVE 几何模型。选取四节点三维实体单元对RVE 几何模型进行网格划分，如图4、5 所示。其中，树脂材料的弹性参数如表2 所示，碳纤维束的弹性参数已通过表2 和式(4)计算得到。

  通常将复合材料层合板假设为正交各向异性材料，其本构关系如式(5)所示。通过对RVE 有限元模型施加6 种不同的载荷条件，解除各参数的耦合关系，求得层合板的弹性参数。各工况条件设置如表3 所示。

  式中，σij和εij分别表示宏观的材料应力与应变张量；Ei、Gij以及μij分别表示层合板各方向的拉伸模量、切变模量以及泊松比。

  以工况1，求解Ex为例。当单胞平面施加正向拉伸位移时，约束单胞在x=0 平面上节点的x 方向的自由度，对x=L 平面施加沿x 方向的位移ΔL。由于单胞模型为复合材料层合板的一部分，为了能够更好的保证单胞模型边界处的变形连续和应力连续，对单胞有限元模型的剩余四个平面施加周期性边界条件。通过仿真计算能得出约束反力Fx，利用式(6)计算出x=0 平面所受的应力

  为了验证计算结果的正确性，将对复合材料层合板进行单轴拉伸及面内剪切试验。单轴拉伸试验参照ASTM-D3039 进行， 面内剪切试验参照ASTM-3518 进行，如图6、7 所示。将层合板弹性参数的预测结果与试验结果对比，如表4 所示，能够准确的看出，计算结果与试验结果很接近，并且含有层合板厚度方向的性能参数，说明采用单胞有限元分析方法能够成功预测出复合材料层合板弹性性能参数。因此，将微观尺度分析中所预测的复合材料弹性参数运用到中尺度分析中是可行的。

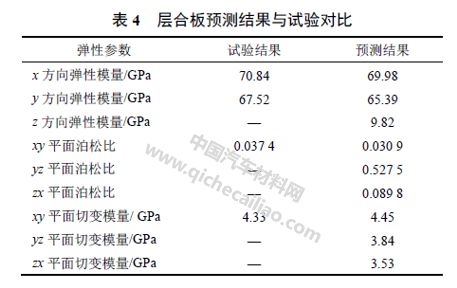
  本节建立的复合材料模型是基于商用有限元软件LS-DYNA 中的MAT_054 模型， 它采用Chang-Chang 失效准则，并且只能应用于壳单元。当全部铺层中的单元发生失效时，该单元被删除。此时，与被删除单元共节点的单元强度被设定的参数减弱。该模型要输入单层板的材料参数，包括密度、三个方向的弹性模量和切变模量、横向及纵向的抗拉和抗压强度、面内剪切强度以及失效应变等。然而，以上材料参数的获取需要进行大量及复杂的试验，这并不适合设计初级阶段的分析。因此，本文利用微观尺度分析中预测的复合材料弹性参数，进一步建立复合材料渐进失效模型，进行中尺度性能分析。所使用的具体参数如表5 所示。

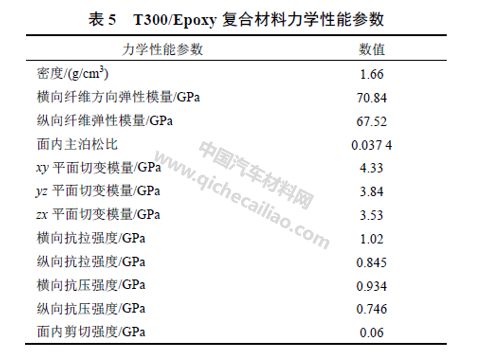
  MAT_54 模型中还包括其他参数，例如ALPH 和BETA，用于定义失效准则，BETA=0 时为最大应力准则，BETA=1 时为Hashin 准则；TFAIL用于定义单元删除的时间步；SOFT 用于对压溃前端的强度进行折减，对轴向压溃仿真的结果有重要影响；FBRT 用于定义基体压缩失效后纤维方向抗压强度的折减系数；YCFAC 用于定义基体压缩失效后纤维方向抗压强度的折减系数。这些参数都无法通过试验获得，只能通过与试验结果对比来调整，直到仿真结果与试验结果吻合。为此， 参照ASTM-D790，对试样进行三点弯曲试验，样件尺寸为10 层，厚度2 mm，如图8 所示。依据此试验结果调整MAT_54 模型的相关参数。

  图 9 为HyperMesh/LS-DYNA 中建立的复合材料三点弯曲数值模拟的有限元模型，试样采用1.5mm×1.5 mm 全积分壳单元进行离散。压头和支座用2 mm×2 mm 的壳单元离散，总共3 216 个单元。其中压头和支座采用刚体材料MAT_20，并约束两个支座的所有自由度。层合板与压头接触类型为“rigid_nodes_to_rigid_body”，通过定义载荷-穿透曲线控制节点所受的法向反力，这对仿真的稳定性起到关键作用。

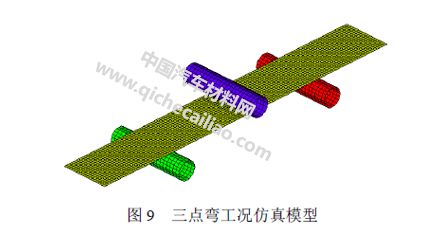
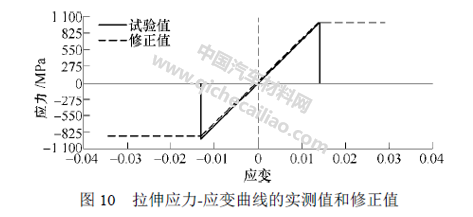
  三点弯曲试验中压头的速度为2 mm/min，为缩短计算时间，数值仿线m/s。由于材料的输入参数都是在准静态工况下获得的，因此加载速度的增加对仿真结果没有影响。对仿真模型参数多次调试，仍然得出与试验不相符的载荷-位移曲线。然而，通过增大材料失效应变即MAT_54 模型中的控制卡片DFAILT 和DFAILC 的值(图10)，得到的三点弯曲数值仿真载荷-位移曲线与试验结果较为接近(图11)。从图11 可看出利用试验获得的应力应变曲线所得到的载荷-位移曲线与利用修正后的应力应变曲线所得到的载荷-位移曲线的区别，显示出了失效应变对仿真结果的影响。

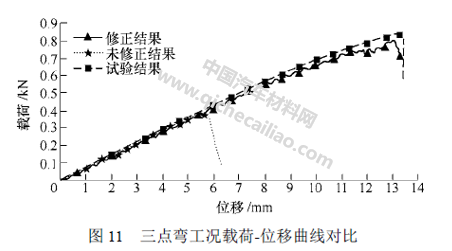
  综上所述，复合材料试样三点弯曲工况的数值模拟结果与试验结果相吻合，说明中尺度分析中所建立的复合材料渐进失效模型是较为准确的，在某些特定的程度上能够模拟复合材料断裂失效行为。因此，可以将该渐进失效本构模型应用于宏观尺度的电动车复合材料车身耐撞性能分析。

  与传统汽车不同，新型电动车分为驱动模块、覆盖件模块以及驾驶舱保护模块。其中，驱动模块最重要的包含电池、驱动系统、电控系统和悬架系统等；覆盖件模块包括门、发罩等覆盖件；驾驶舱保护模块是由高强度、轻质复合材料制成，在受到撞击时能够保护驾驶员及乘客的安全。

  该复合材料车身应用所采用的生产的基本工艺与传统的金属车身不同。新型复合材料车身的制造可采用树脂转移技术先加工尺寸较小的零部件，再将其粘结成一个更大的组分，最终在模具中结合成整体车身；这使得零部件的总数较传统金属车身大为减少。尽管目前复合材料成本及其零部件制造工艺成本较传统金属材料而言还相比来说较高，但是由于其优良的力学性能及其在轻量化方面的突出表现，使得复合材料在汽车上的应用成为一种必然的趋势。

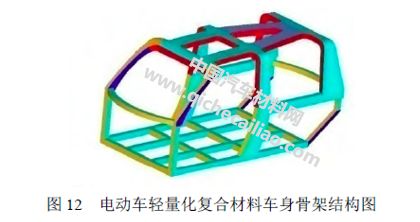
  本文所研究的新型复合材料车身由斜纹机织复合材料，用三通、四通接头连接成的笼型结构，如图12 所示。下面将利用中尺度分析中经过验证的MAT_54 复合材料渐进失效模型，对车身骨架的耐撞性能进行分析。

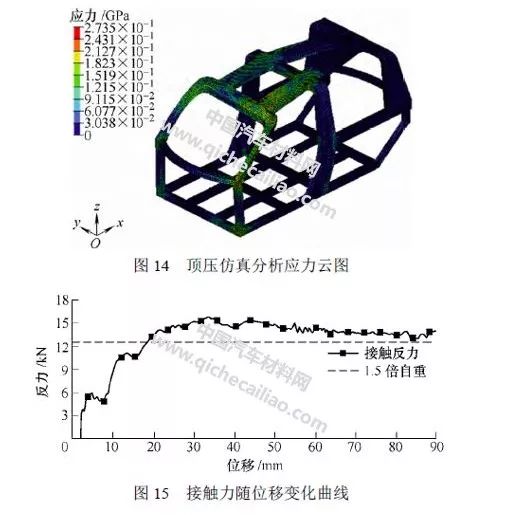
  参考美国联邦汽车安全标准(FMVSS 216)进行顶压仿真分析，其目的是模拟翻车状态顶盖在受到自重1.5 倍作用下，顶盖强度应能保证乘员的最小生存空间，要求顶盖变形小于127 mm。顶压仿线 所示。

  计算结果如图14 所示，从图14 能够准确的看出，最大平均应力为273.5 MPa，小于层合板抗拉强度1 020 MPa；图15 为刚性墙的接触力随位移变化曲线 可知当刚性墙接触力增大至1.5 倍自重(12.54 kN)时，刚性墙沿其法线mm，远小于法规要求的127 mm。

  为了考察复合材料车身骨架的性能，根据EuroNCAP法规进行柱碰仿真分析。该测试的目的是在柱碰过程中考察驾驶舱的变形以及对乘员头部的伤害。

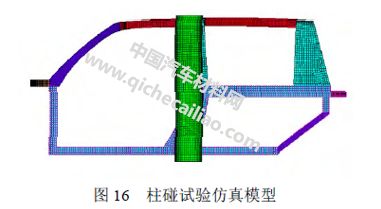
  采用 20 mm×20 mm 全积分壳单元对复合材料车身骨架进行离散，共29 975 个单元。在LS-DYNA中的MAT_54 中将复合材料属性定义为10 层(沿厚度方向积分点为10 个)，厚度为2 mm。将整车质量附加在车身骨架下部，并将整车加速到29 km/h，使其与固定的直径为254 mm 的刚性圆柱撞击，撞击点x 方向的坐标值与电动车H 点的x 方向坐标值一致，如图16 所示。在B 柱上选取15 个测量点，考察其在碰撞过程中的最大变形。

  为了更好地反映出复合材料车身骨架的耐撞性能，还针对厚度为3 mm 的铝合金车身骨架做多元化的分析，并与复合材料骨架性能作对比。两模型中，所选取的相同参考点在碰撞过程中的最大变形值构成的曲线 可知，碰撞过程中铝合金骨架比复合材料骨架产生的变形大。其中，复合材料骨架的顶盖、窗框以及门槛处的最大变形分别为64.6 mm、128.4 mm、214.6 mm；而铝合金相应位置的最大变形分别为88.3 mm、203.6 mm、340.2 mm。图18 和图19 分别为复合材料车身骨架和铝合金车身骨架的最大变形图。由图18、19 可知，最大变形位于车身骨架下部与刚性柱相接触的接头处。由于该位置与刚性柱非间接接触，并且接头部位会造成应力集中，导致复合材料单元失效，从而使得该处的变形最大。经对比分析表明，复合材料车身骨架较铝合金骨架在重量减轻59%的同时，展现了更好的耐撞性能。

  根据斜纹机织复合材料细观几何结构，建立了其单胞模型，利用有限元的方法对复合材料层合板的三维弹性性能进行预测，并通过试验验证，证明了该预测方法较为准确。利用LS-DYNA 中的MAT_54 并结合层合板的性能参数，建立复合材料模型，参考三点弯曲试验结果对复合材料模型参数做调整，最终得到准确的复合材料渐进失效模型。将调整好的复合材料渐进失效模型应用到电动车骨架性能分析中。通过顶压仿真分析得出，加载过程中最大平均应力远小于材料的抗拉强度，并且当接触力达到1.5 倍自重时，刚性墙沿其发现方向挪动18.3 mm，满足法规要求。在柱碰仿真分析过程中与铝合金骨架作对比，通过选取相同位置的测量点的侵入量能够准确的看出，复合材料骨架的侵入量小于铝合金骨架，并且复合材料车身骨架较铝合金骨架重量减轻59%。由此能够看出，多尺度的分析方法，可以轻松又有效地应用到电动车复合材料轻量化设计中。